Visualizing Growth Using World Bank Development Indicators¶
Sean McSkeane, Albert Chu, Sonny Liu
Table of Contents¶
- Background
- Introduction
- Defintions
- Libraries
- Context
- Data Processing
- Data Collection
- Creation of GDP Data
- Creation of Miscellaneous Data
- Exploratory Analysis and Data Visualization
- GDP Statistics
- GDP Box Plots
- Observations
- Miscellaneous Joint Plots
- Observations
- Analysis, Hypothesis Testing, and Machine Learning
- Linear Regression
- Insight and Policy Design
- Summary
- Insight
Background
1.0 Introduction¶
Economists are constantly making predictions about world economies with economic models and forecasts. In this analysis, we attempt to correlate the percentage growth of GDP per capita for nations using data provided by the World Bank. The World Bank is an international financial institution based in Washington D.C. that provides loans and grants to the governments of poorer countries for the purpose of pursuing capital projects. One of the major goals of the World Bank is to end extreme poverty in developing nations.
We use data provided from the World Bank's World Development Indicators to create our own custom comma-separated values (CSV) file for our own data analysis. According to the World Bank's website, "World Development Indicators (WDI) is the primary World Bank collection of development indicators, compiled from officially recognized international sources. It presents the most current and accurate global development data available, and includes national, regional and global estimates."
In our analysis we visualize the growth of world economies by cleaning and reorganizing, plotting important economic factors across time, correlating other factors with gdp per capita, and using machine learning to predict future growth.
1.1 Definitions¶
Here are definitions of the datapoints we use directly taken from the World Bank.
GDP:
GDP stands for gross domestic product. It is used to measure the market value of all the final goods and services produced in a specific time period.
Per Capita:
Per capita simply is an economic term that means per person in a specefied area.
Final Consumption Expenditure:
Final consumption expenditure (formerly total consumption) is the sum of household final consumption expenditure (private consumption) and general government final consumption expenditure (general government consumption). This estimate includes any statistical discrepancy in the use of resources relative to the supply of resources.
General government final consumption expenditure (current US$):
General government final consumption expenditure (formerly general government consumption) includes all government current expenditures for purchases of goods and services (including compensation of employees). It also includes most expenditures on national defense and security, but excludes government military expenditures that are part of government capital formation. Data are in current U.S. dollars.
Foreign direct investment, net inflows (BoP, current US$):
Foreign direct investment refers to direct investment equity flows in the reporting economy. It is the sum of equity capital, reinvestment of earnings, and other capital. Direct investment is a category of cross-border investment associated with a resident in one economy having control or a significant degree of influence on the management of an enterprise that is resident in another economy. Ownership of 10 percent or more of the ordinary shares of voting stock is the criterion for determining the existence of a direct investment relationship. Data are in current U.S. dollars.
Exports of goods and services (current US$):
Exports of goods and services comprise all transactions between residents of a country and the rest of the world involving a change of ownership from residents to nonresidents of general merchandise, net exports of goods under merchanting, nonmonetary gold, and services. Data are in current U.S. dollars.
Imports of goods and services (current US$):
Imports of goods and services comprise all transactions between residents of a country and the rest of the world involving a change of ownership from nonresidents to residents of general merchandise, nonmonetary gold, and services. Data are in current U.S. dollars.
1.2 Libraries¶
The following python libraries used are listed below along with their official descriptions:
- pandas - an open source, BSD-licensed library providing high-performance, easy-to-use data structures and data analysis tools for the Python programming language (docs)
- numpy - NumPy is the fundamental package for scientific computing with Python (docs)
- matplotlib - Matplotlib is a Python 2D plotting library which produces publication quality figures in a variety of hardcopy formats and interactive environments across platforms (docs)
- seaborn - Seaborn is a Python data visualization library based on matplotlib. It provides a high-level interface for drawing attractive and informative statistical graphics (docs)
- sklearn - Scikit-learn is an open source machine learning library that supports supervised and unsupervised learning. It also provides various tools for model fitting, data preprocessing, model selection and evaluation, and many other utilities (docs)
- statsmodels - is a Python module that provides classes and functions for the estimation of many different statistical models, as well as for conducting statistical tests, and statistical data exploration (docs)
- folium - makes it easy to visualize data that’s been manipulated in Python on an interactive leaflet map. (docs)
import pandas as pd
from pandas.io.json import json_normalize
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import linear_model
from sklearn.preprocessing import PolynomialFeatures
from sklearn import model_selection
from statsmodels import api as sm
import folium
import json
1.3 Context¶
According to investopedia, "Economic forecasting is the process of attempting to predict the future condition of the economy using a combination of important and widely followed indicators. Economic forecasting involves the building of statistical models with inputs of several key variables, or indicators, typically in an attempt to come up with a future gross domestic product (GDP) growth rate. Primary economic indicators include inflation, interest rates, industrial production, consumer confidence, worker productivity, retail sales, and unemployment rates."
Economic predicitons are incredibly important for buisnesses and governments world wide. They want to manage their finances accoridingly so that they can encourage growth and mitigate losses. However, many descriped economic forecasting as unreliable. Investopedia goes on to even state that "Economic forecasting is often described as a flawed science." According to Bloomberg Buisness, "A recent working paper by Zidong An, Joao Tovar Jalles, and Prakash Loungani discovered that of 153 recessions in 63 countries from 1992 to 2014, only five were predicted by a consensus of private-sector economists in April of the preceding year." This shows that economies are far too complex for even large agencies to forecast accurately, and that economic models are often misleading.
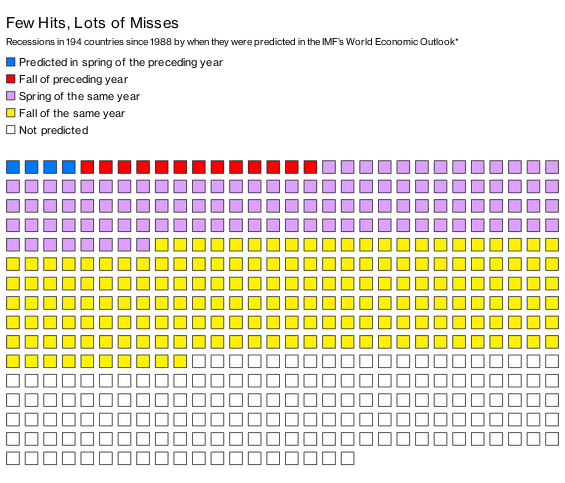source from Bloomberg Buisness
In this project, we attempt to correlate GDP growth with several important key data points. This project will help us to get an intuition at the challenges economists face and also to see how far data science and programming can help amateurs like ourselves tackle on national economies.
Data Processing
2.0 Data Collection¶
The formula for calculating GDP is:
GDP = Consumption + Investment + Government Spending + Net Exports
therefore we concluded it would be best if we split the CSV into two dataframes which included GDP calculators and another dataframe from more miscellenous data.
We searched through the World Bank Development Indicators in order to find datapoints that matched the formula as close as possible. We also chose datapoints that we found interesting and/or could possibly have a correlation with GDP per capita and GDP growth. Our datset is availble here at the project's github page.
worldBankDevInc = pd.read_csv("WorldBankData/data.csv")
worldBankDevInc.dropna(inplace=True)
countryName = ""
first = True
newRows = []
countriesData = []
for index, row in worldBankDevInc.iterrows():
if (countryName != row["Country Name"]):
if (first == False):
countriesData.append(df)
countryName = row["Country Name"]
df = pd.DataFrame(columns=worldBankDevInc.columns)
first = False
df = df.append(row, ignore_index=True)
worldData = pd.concat(countriesData)
with pd.option_context('display.max_rows', None, 'display.max_columns', None):
display(df)
display(countriesData[206])
Above are two raw dataframes of the data from the the CSV file obtained from the world bank. One of them shows world statistics and the other shows statistics from the United States. The list contriesData in our code simply contains a dataframe for each country or region that the World Bank provides. If you wish to see a certain country you can change the index of display(CountriesData[n]) to be whatever country you wish to see.
2.1 Creation of GDP Data¶
The predictionData dataframe consists of variables that are known to calculate GDP. The dataframe was built using the worldData dataframe and consists of columns for country, year, GDP per capita (current US), GDP per capita growth (annual percentage), final consumption expenditure (percentage of GDP), final consumption expenditure (current US), general government final consumption expenditure (current US), general government final consumption expenditure (percentage of GDP), foreign direct investment, net inflows (percentage of GDP), foreign direct investment, net inflows (BoP, current US), exports of goods and services (current US), imports of goods and services (current US), exports of goods and services (percentage of GDP), and imports of goods and services (% of GDP).
The dataframe contains one row for each combination of country and year, with the remaining values in the row corresponding to the variables listed above. This was done to enable easy plotting when analyzing the data. However, only years from 2000 to 2015 were included to ensure minimal missing data, as years prior to 2000 were more likely to be missing data. An important factor to note that it is there was no data point calculating total investments for any nation. Therefore we used one metric of investment which was Foreign Direct Investment as an indicator of investment for a country.
predictionData = pd.DataFrame(columns = ["Country Name", "Year"])
countriesList = worldData["Country Name"]
for name in countriesList.unique():
counter = 2000
while counter <= 2015:
predictionData = predictionData.append({"Country Name": name, "Year": counter}, ignore_index=True)
counter += 1
predictionData["GDP per capita (current US$)"] = 0.0
predictionData["GDP per capita growth (annual %)"] = 0.0
predictionData["Final consumption expenditure (% of GDP)"] = 0.0
predictionData["Final consumption expenditure (current US$)"] = 0.0
predictionData["General government final consumption expenditure (current US$)"] = 0.0
predictionData["General government final consumption expenditure (% of GDP)"] = 0.0
predictionData["Foreign direct investment, net inflows (% of GDP)"] = 0.0
predictionData["Foreign direct investment, net inflows (BoP, current US$)"] = 0.0
predictionData["Exports of goods and services (current US$)"] = 0.0
predictionData["Imports of goods and services (current US$)"] = 0.0
predictionData["Exports of goods and services (% of GDP)"] = 0.0
predictionData["Imports of goods and services (% of GDP)"] = 0.0
predictionData["GDP growth (annual %)"] = 0.0
country = "Afghanistan"
countryCounter = 0
for index, row in worldData.iterrows():
if row["Country Name"] != country:
countryCounter += 1
country = row["Country Name"]
if row["Series Name"] in predictionData.columns:
counter = 2000
while counter <= 2015:
yearString = str(counter) + " [YR" + str(counter) + "]"
indx = countryCounter * 16 + (counter - 2000)
if row[yearString] != "..":
predictionData.at[indx, row["Series Name"]] = row[yearString]
else:
predictionData.at[indx, row["Series Name"]] = np.nan
counter += 1
predictionData.drop(predictionData.index[3472:], inplace=True)
predictionData
2.2 Creation of Miscellenous Data¶
The miscellaneousData dataframe consists of variables we thought would have a correlation to GDP growth. The dataframe was built using the worldData dataframe and consists of columns for country, year, GDP per capita (current US), employment in agriculture (% of total employment) (modeled ILO estimate), employment in industry (% of total employment) (modeled ILO estimate), employment in services (% of total employment) (modeled ILO estimate), current health expenditure (% of GDP), fertility rate, total (births per woman), government expenditure on education, total (% of GDP), prevalence of undernourishment (% of population), adjusted net enrollment rate, primary (% of primary school age children).
The dataframe contains one row for each combination of country and year, with the remaining values in the row corresponding to the variables listed above. This was done to enable easy plotting when analyzing the data. However, only years from 2000 to 2015 were included to ensure minimal missing data, as years prior to 2000 were more likely to be missing data.
miscellaneousData = pd.DataFrame(columns = ["Country Name", "Year"])
countriesList = worldData["Country Name"]
for name in countriesList.unique():
counter = 2000
while counter <= 2015:
miscellaneousData = miscellaneousData.append({"Country Name": name, "Year": counter}, ignore_index=True)
counter += 1
miscellaneousData["GDP per capita (current US$)"] = 0.0
miscellaneousData["Employment in agriculture (% of total employment) (modeled ILO estimate)"] = 0.0
miscellaneousData["Employment in industry (% of total employment) (modeled ILO estimate)"] = 0.0
miscellaneousData["Employment in services (% of total employment) (modeled ILO estimate)"] = 0.0
miscellaneousData["Current health expenditure (% of GDP)"] = 0.0
miscellaneousData["Fertility rate, total (births per woman)"] = 0.0
miscellaneousData["Government expenditure on education, total (% of GDP)"] = 0.0
miscellaneousData["Prevalence of undernourishment (% of population)"] = 0.0
miscellaneousData["Adjusted net enrollment rate, primary (% of primary school age children)"] = 0.0
country = "Afghanistan"
countryCounter = 0
for index, row in worldData.iterrows():
if row["Country Name"] != country:
countryCounter += 1
country = row["Country Name"]
if row["Series Name"] in miscellaneousData.columns:
counter = 2000
while counter <= 2015:
yearString = str(counter) + " [YR" + str(counter) + "]"
indx = countryCounter * 16 + (counter - 2000)
if row[yearString] != "..":
miscellaneousData.at[indx, row["Series Name"]] = row[yearString]
else:
miscellaneousData.at[indx, row["Series Name"]] = np.nan
counter += 1
miscellaneousData.drop(predictionData.index[3472:], inplace=True)
miscellaneousData
Exploratory Analysis and Data Visualization
3.0 GDP Statistics¶
The following table below provides us with the statistics from the variables that are involved with calculating GDP. These only utilize the information contained in data for calculating GDP.
predictionData.describe()
Although this information is useful to look at when looking at the big picture, it would be more interesting to see how these variables have changed overtime. In the boxplots below we seperate each datapoint as its own boxplot and plot them by five year intervals.
3.1 GDP Box Plots¶
The box plot below shows that although the median GDP per capita has slowly been increasing, the wealthiest 50\% of nations are making significantly more progress than the poorest 50 \% of nations. According to Investopedia, "As a rule of thumb, countries with developed economies have GDP per capitas of at least \$12,000(USD), although some economists believe \\$25,000 (USD) is a more realistic measurement threshold." As shown below, most only about 25-50\% of countries are considered developed depending on what your threshold is for developed countries.
sns.set(rc={'figure.figsize':(15,10)})
box = sns.boxplot(x="Year", y="GDP per capita (current US$)", data=predictionData, showfliers=False).set_title("Year vs. GDP per capita")
The box plot below has shown how GDP and GDP per capita has grown throughout the years. As you can see there is a large drop in 2009 due to the great recession. Otherwise GDP growth has stayed very consistent in terms of growth throughout the years.
sns.set(rc={'figure.figsize':(15,10)})
box = sns.boxplot(x="Year", y="GDP growth (annual %)", data=predictionData, showfliers=False).set_title("Year vs. GDP growth (annual %)")
sns.set(rc={'figure.figsize':(15,10)})
box = sns.boxplot(x="Year", y="GDP per capita growth (annual %)", data=predictionData, showfliers=False).set_title("Year vs. GDP per capita growth (annual %)")
sns.set(rc={'figure.figsize':(15,10)})
box = sns.boxplot(x="Year", y="Final consumption expenditure (current US$)", data=predictionData, showfliers=False).set_title("Year vs. Final consumption expenditure")
sns.set(rc={'figure.figsize':(15,10)})
box = sns.boxplot(x="Year", y="General government final consumption expenditure (current US$)", data=predictionData, showfliers=False).set_title("Year vs. General government final consumption expenditure")
sns.set(rc={'figure.figsize':(15,10)})
box = sns.boxplot(x="Year", y="Foreign direct investment, net inflows (BoP, current US$)", data=predictionData, showfliers=False).set_title("Year vs. Foreign direct investment, net inflows (BoP, current US$)")
sns.set(rc={'figure.figsize':(15,10)})
box = sns.boxplot(x="Year", y="Exports of goods and services (current US$)", data=predictionData, showfliers=False).set_title("Exports of goods and services (current US$)")
sns.set(rc={'figure.figsize':(15,10)})
box = sns.boxplot(x="Year", y="Imports of goods and services (current US$)", data=predictionData, showfliers=False).set_title("Imports of goods and services (current US$)")
3.2 Observations from GDP Data¶
From the box plots we are able to observe that although every economy is improving in every single category, the countries in the top 50 \% are improving at a much greater rate than the other countries in the bottom 50\%. However this can also be attributed to the fact that countries with lower GDPs won't grow as quickly quantitativly because they start out off with lower economical stock. If we plot out the GDP growth by annual percentage for nations that are high income and nations from the least developed countries, we'll see that the nations from the least developed countries are growing at a faster rate. In fact according to the Nasdq, the five fastest growing nations are all in developing countries.
richvsPoor = pd.DataFrame(columns = ["Country Name", "Year"])
countriesList = worldData["Country Name"]
for name in countriesList.unique():
counter = 2000
while counter <= 2015:
richvsPoor = richvsPoor.append({"Country Name": name, "Year": counter}, ignore_index=True)
counter += 1
richvsPoor["GDP growth (annual %)"] = 0.0
country = "Afghanistan"
countryCounter = 0
for index, row in worldData.iterrows():
if row["Country Name"] != country:
countryCounter += 1
country = row["Country Name"]
if row["Series Name"] in richvsPoor.columns:
counter = 2000
while counter <= 2015:
yearString = str(counter) + " [YR" + str(counter) + "]"
indx = countryCounter * 16 + (counter - 2000)
if row[yearString] != "..":
richvsPoor.at[indx, row["Series Name"]] = row[yearString]
else:
richvsPoor.at[indx, row["Series Name"]] = np.nan
counter += 1
graphData = pd.DataFrame(columns=richvsPoor.columns)
graphData2 = pd.DataFrame(columns=richvsPoor.columns)
richvsPoor.drop(richvsPoor.index[:3696], inplace=True)
for index, row in richvsPoor.iterrows():
if row["Country Name"] == "Least developed countries: UN classification":
graphData = graphData.append(row, ignore_index=True)
elif row["Country Name"] == "High income":
graphData2 = graphData2.append(row, ignore_index=True)
sns.set(rc={'figure.figsize':(15,10)})
box = sns.lineplot(x="Year", y="GDP growth (annual %)", data=graphData).set_title("Growth of least developed countries")
sns.set(rc={'figure.figsize':(15,10)})
box = sns.lineplot(x="Year", y="GDP growth (annual %)", data=graphData2).set_title("Growth of most developed countries")
This is due in part because of the solow model. According to the University of Pittsburgh.
“If the Solow model is correct, and if growth is due to capital accumulation , we should expect to find
Growth will be very strong when countries first begin to accumulate capital, and will slow down as the process of accumulation continues. Japanese growth was stronger in the 1950s and 1960s than it is now. Countries will tend to converge in output per capita and in standard of living. As Hong Kong, Singapore, Taiwan (etc) accumulate capital, their standard of living will catch up with the initially more developed countries. When all countries have reached a steady state, all countries will have the same standard of living (at least if they have the same production function, which for most industrial goods is a reasonable assumption).”
This model helps explain why poorer countries are growing their economies at a faster rate than their developed nations. Of course there are always exceptions and in some cases developed countries grow faster than developing ones, but the general trend still exists.
3.3 Miscellaneous Joint Plots¶
The following table below provides us with the statistics from the miscellaneous variables that we thought would correlate to GDP.
miscellaneousData.describe()
To illustrate the relationship between the miscellaneous variables and GDP per capita, we used joint plots, which are a combination of one scatter plot representing the correlation and two bar plots representing the Gaussian distribution of each of the variables respectively. The joint plots show correlation between several key data points and the GDP per capita of countries.
sns.set(rc={'figure.figsize':(15,10)})
joint = sns.jointplot(x="Employment in agriculture (% of total employment) (modeled ILO estimate)", y="GDP per capita (current US$)", data=miscellaneousData, height = 13)
sns.set(rc={'figure.figsize':(15,10)})
joint = sns.jointplot(x="Employment in industry (% of total employment) (modeled ILO estimate)", y="GDP per capita (current US$)", data=miscellaneousData, height = 13)
sns.set(rc={'figure.figsize':(15,10)})
joint = sns.jointplot(x="Employment in services (% of total employment) (modeled ILO estimate)", y="GDP per capita (current US$)", data=miscellaneousData, height = 13)
sns.set(rc={'figure.figsize':(15,10)})
joint = sns.jointplot(x="Current health expenditure (% of GDP)", y="GDP per capita (current US$)", data=miscellaneousData, height = 13)
sns.set(rc={'figure.figsize':(15,10)})
joint = sns.jointplot(x="Fertility rate, total (births per woman)", y="GDP per capita (current US$)", data=miscellaneousData, height = 13)
sns.set(rc={'figure.figsize':(15,10)})
joint = sns.jointplot(x="Prevalence of undernourishment (% of population)", y="GDP per capita (current US$)", data=miscellaneousData, height = 13)
sns.set(rc={'figure.figsize':(15,10)})
joint = sns.jointplot(x="Adjusted net enrollment rate, primary (% of primary school age children)", y="GDP per capita (current US$)", data=miscellaneousData, height = 13)
3.4 Observations from Miscellaneous Data¶
There are some obvious correlations between GDP per capita and data points such as undernourishment, primary school enrollment, and the fertility rate. But there were also a couple of interesting caveats that were less obvious. For example, nations that had low GDP per capitas tended to have high percentages of its workforce in the agricultural industry. Also nations that had high GDP per capitas tended to have high percentages of its workforce in the service industry. But there was a healthy mix of economies when it came to high percentages of their workforce in industry. Some nations with high industry employment came from relatively rich countries and some places from very poor nations had high levels of employment in industry. The general trend was still that developing nations with their GDP per capitas near the average tended to have the most concentration on industry work. Also nations that tended to spend more of their % of GDP on healthcare tended to be richer nations rather than poorer ones, although the correlation for that data point was not as strong.
Analysis, Hypothesis Testing, and Machine Learning
4.0 Linear Regression¶
For the analysis, hypothesis testing, and machine learning part of this tutorial, we will be performing linear regression to model our data and thus better observe how different factors influence GDP.
To do so, we must organize the data used for the box plots (predictionData) from earlier since we will be first do linear regressions on GDP per capita, final consumption expenditure, general government final consumption expenditure, foreign direct investment, exports and imports of goods and services. We do this by copying predictionData into a separate dataframe, dropping irrelevant columns including CountryName, and grouping the data by year such that we get the mean for GDP per capita, final consumption expenditure, general government final consumption expenditure, foreign direct investment, exports and imports of goods and services for each year.
linearData = predictionData.copy()
linearData = linearData.drop(columns=['Country Name', 'GDP per capita growth (annual %)', 'Final consumption expenditure (% of GDP)', 'General government final consumption expenditure (% of GDP)', 'Foreign direct investment, net inflows (% of GDP)', 'Exports of goods and services (% of GDP)', 'Imports of goods and services (% of GDP)' , 'GDP growth (annual %)'])
linearData = linearData.groupby(['Year']).mean()
linearData
Now, we may perform linear regression on GDP per capita (current USD) over time by creating a scatter plot containing years on the x-axis and GDP per capita (current USD) on the y-axis and then fitting a best fit line using LinearRegression() over the scatter plot.
text = "GDP per capita (current US$)"
years = []
GDP_per_capita = []
for index, row in linearData.iterrows():
years.append(index)
GDP_per_capita.append(row[0])
plt.plot(years,GDP_per_capita,'o')
years_ = []
for y in years:
years_.append([y])
clf = linear_model.LinearRegression()
clf.fit(years_,GDP_per_capita)
predicted = clf.predict(years_)
plt.plot(years,predicted)
plt.title("{} over time".format(text))
plt.xlabel("Year")
plt.ylabel("GDP per capita (current US$)")
plt.show()
In the resulting plot, we can clearly see a positive trend from just the scatter plot alone, and the linear model confirms this since it produces a linear line with a positive slope. Thus, we can confirm that GDP per capita grows over time.
Next, we will find the R^2 value to see how well the linear regression fits our data by using clf.score().
print(clf.score(years_,GDP_per_capita))
Our results show R^2 being 0.848 which means that the linear regression fits the data pretty well as it is closer to 1 which signifies a perfect fit than 0 which means no meaningful fit.
Moving on, we must observe the fact that our scatter plot seems to flatten after 2010, so we must see if a polynomial of 2 degrees fits our data better.
plt.plot(years,GDP_per_capita,'o')
polynomial_Feats = PolynomialFeatures(degree=2)
polynomial_years = polynomial_Feats.fit_transform(years_)
clf.fit(polynomial_years,GDP_per_capita)
polynomial_predict = clf.predict(polynomial_years)
plt.title("{} over time".format(text))
plt.xlabel("Year")
plt.ylabel("GDP per capita (current US$)")
plt.plot(years,polynomial_predict)
plt.show()
print(clf.score(polynomial_years,GDP_per_capita))
Here we have a R^2 value of 0.944 which is much better than our linear fit.
Now we can try a polynomial with 3 degrees.
plt.plot(years,GDP_per_capita,'o')
polynomial_Feats = PolynomialFeatures(degree=3)
polynomial_years = polynomial_Feats.fit_transform(years_)
clf.fit(polynomial_years,GDP_per_capita)
polynomial_predict = clf.predict(polynomial_years)
plt.title("{} over time".format(text))
plt.xlabel("Year")
plt.ylabel("GDP per capita (current US$)")
plt.plot(years,polynomial_predict)
plt.show()
print(clf.score(polynomial_years,GDP_per_capita))
Now we have an R^2 value of 0.956 which is slightly better than the last. However, must must take into account that the curve downwards seems to be heavily influenced by one data point on the scatter plot.
Next, we can repeat the process of fitting linear regressions to final consumption expenditure, general government final consumption expenditure, foreign direct investment, exports and imports of goods and services.
def plot_GDP_predictors(x,y,linearData):
years = []
GDP_predictor = []
for index, row in linearData.iterrows():
years.append(index)
GDP_predictor.append(row[y])
plt.plot(years,GDP_predictor,'o')
years_ = []
for y in years:
years_.append([y])
clf = linear_model.LinearRegression()
clf.fit(years_,GDP_predictor)
predicted = clf.predict(years_)
plt.title("{} over time".format(x))
plt.xlabel("Year")
plt.ylabel(x)
r_squared = clf.score(years_,GDP_predictor)
plt.plot(years,predicted,label="linear-regression R^2:{}".format(round(r_squared,2)))
plt.legend()
plt.show()
plt.plot(years,GDP_predictor,'o')
polynomial_Feats = PolynomialFeatures(degree=2)
polynomial_years = polynomial_Feats.fit_transform(years_)
clf.fit(polynomial_years,GDP_predictor)
polynomial_predict = clf.predict(polynomial_years)
plt.title("{} over time".format(x))
plt.xlabel("Year")
plt.ylabel(x)
plt.plot(years,polynomial_predict)
plt.show()
print(clf.score(polynomial_years,GDP_predictor))
polynomial_Feats = PolynomialFeatures(degree=3)
polynomial_years = polynomial_Feats.fit_transform(years_)
clf.fit(polynomial_years,GDP_predictor)
polynomial_predict = clf.predict(polynomial_years)
plt.title("{} over time".format(x))
plt.xlabel("Year")
plt.ylabel(x)
plt.plot(years,polynomial_predict)
plt.show()
print(clf.score(polynomial_years,GDP_predictor))
plot_GDP_predictors("Final consumption expenditure (current US$)",1,linearData)
plot_GDP_predictors("General government final consumption expenditure (current US$)",2,linearData)
plot_GDP_predictors("Foreign direct investment, net inflows (BoP, current US$)",3,linearData)
plot_GDP_predictors("Exports of goods and services (current US$)",4,linearData)
plot_GDP_predictors("Imports of goods and services (current US$)",5,linearData)
Our results show that final consumption expenditure, general government final consumption expenditure, foreign direct investment net inflows, exports and imports of goods and services all trend upwards, but it is important to note that the R^2 value for foreign direct investment, net inflows is sub 0.5
Next, we can repeat the same process for linear regression with our data from miscelleaneousData.
linearmiscData = miscellaneousData.copy()
linearmiscData = linearmiscData.drop(columns=['Country Name'])
linearmiscData = linearmiscData.groupby(['Year']).mean()
linearmiscData
def plot_GDP_misc(x,y,linearmiscData):
years = []
GDP_predictor = []
for index, row in linearmiscData.iterrows():
years.append(index)
GDP_predictor.append(row[y])
plt.plot(years,GDP_predictor,'o')
years_ = []
for y in years:
years_.append([y])
clf = linear_model.LinearRegression()
clf.fit(years_,GDP_predictor)
predicted = clf.predict(years_)
plt.title("{} over time".format(x))
plt.xlabel("Year")
plt.ylabel(x)
r_squared = clf.score(years_,GDP_predictor)
plt.plot(years,predicted,label="linear-regression R^2:{}".format(round(r_squared,2)))
plt.legend()
plt.show()
plt.plot(years,GDP_predictor,'o')
polynomial_Feats = PolynomialFeatures(degree=2)
polynomial_years = polynomial_Feats.fit_transform(years_)
clf.fit(polynomial_years,GDP_predictor)
polynomial_predict = clf.predict(polynomial_years)
plt.title("{} over time".format(x))
plt.xlabel("Year")
plt.ylabel(x)
plt.plot(years,polynomial_predict)
plt.show()
print(clf.score(polynomial_years,GDP_predictor))
polynomial_Feats = PolynomialFeatures(degree=3)
polynomial_years = polynomial_Feats.fit_transform(years_)
clf.fit(polynomial_years,GDP_predictor)
polynomial_predict = clf.predict(polynomial_years)
plt.title("{} over time".format(x))
plt.xlabel("Year")
plt.ylabel(x)
plt.plot(years,polynomial_predict)
plt.show()
print(clf.score(polynomial_years,GDP_predictor))
plot_GDP_predictors("Employment in agriculture (% of total employment) (modeled ILO estimate)",1,linearmiscData)
plot_GDP_predictors("Employment in industry (% of total employment) (modeled ILO estimate)",2,linearmiscData)
plot_GDP_predictors("Employment in services (% of total employment) (modeled ILO estimate)",3,linearmiscData)
plot_GDP_predictors("Current health expenditure (% of GDP)",4,linearmiscData)
plot_GDP_predictors("Fertility rate, total (births per woman)",5,linearmiscData)
plot_GDP_predictors("Government expenditure on education, total (% of GDP)",6,linearmiscData)
plot_GDP_predictors("Prevalence of undernourishment (% of population)",7,linearmiscData)
plot_GDP_predictors("Adjusted net enrollment rate, primary (% of primary school age children)",8,linearmiscData)
Results here show that employment in agriculture trends downwards over time, employment in industry over time cannot be conclusive, employment in services trends upwards over time, current health expenditure trends upwards over time, fertility rate trends downwards over time, government expenditure in education over time is not conclusive, prevalence of undernourishment trends downwards over time, and adjusted net enrollment rate trends upwards over time.
Insight and Policy Decision
5.0 Summary¶
For this project, we wanted to analyze the effect that various data points have on the economies of different countries. In order to do this we first collected data from the World Bank data set that included variables that are known to calculate GDP as well as some miscellaneous variables that we thought could be used to visualize GDP growth. We then broke this data into two different data frames, with one representing the variables used to calculate GDP and the other representing the variables we thought could be used to visualize GDP. The data frames were then transformed, so that the columns consisted of variables, with each row representing an instance of a country and a year. We then performed analyses on the two data frames by plotting the correlation between the different variables to GDP per capita. Linear regression was then used for in-depth analysis as we tried to visualize the growth of GDP in countries over time.
5.1 Insight¶
With this data we concluded some aspects of economics which we were already aware of and found out some information that suprised us. For example, there was very little correlation between GDP per capita and the percentage of GDP spent on education. But our predicitons about lower birth rates in more developed countries shown to be supported by the data we plotted. Visualizing economics through data science is an extremely important field, and the large amount of information organizations such as the World Bank and the IMF give solidifies that. With this information, economists can attempt to form more accurate models and predictions that could impact billions of people. Hopefully, this tutorial has allowed you to get a glimpse on the potential visualizing databanks such as these can have on our perceptions and decisions regarding important economic topics.